Ein Algorithmus ist eine eindeutige Handlungsvorschrift zur Lösung eines Problems oder einer Klasse von Problemen. Algorithmen bestehen aus endlich vielen, wohldefinierten Einzelschritten. Algortihmen müssen eindeutig (einzelne Schritte und ihre Abfolge sind unmissverständlich beschrieben), allgemein (lösen nicht nur ein Problem, sondern eine ganze Klasse von Problemen), ausführbar (Menschen oder Maschinen müssen die Einzelschritte abarbeiten können) und endlich (begrenzte Anzahl von Anweisungen mit begrenzter Länge) sein.
Es kann mehrere Algorithmen geben die das gleiche Problem lösen. Diese unterscheiden sich aber in der Regel darin ob sie das Problem rekursion oder iterativ lösen, ob sie die Daten in-place oder out-of-place verarbeiten und haben unterschiedliche gute Laufzeitkomplexitäten.
Rekursion ist ein Programmierkonzept, bei dem eine Funktion einen kleinen Teil des Problems löst und sich dann selbst aufruft um das Problem weiter zu verkleinern. Das wird so lange wiederholt bis das Problem komplett gelöst ist. Um eine unendliche Rekursion zu verhindert muss unbedingt eine Abbruchbedingung definiert werden. Bei Funktions- oder Methodenaufrufen werden die Rücksprungadresse und ggf. Parameter und lokale Variablen im Arbeitsspeicher auf dem Stack abgelegt. Je tiefer die Rekursion desto höher wächst der Stack an. Wenn die Rekursion zu tief ist und der für den Stack reservierte Arbeitspeicher nicht mehr ausreicht, kommt es zu einem Stacküberlauf (stack overflow). Das kann zum Absturz des Prozesses führen.
package main
import "fmt"
func fakultaet(n int) int {
if n == 0 {
return 1
} else {
return n * fakultaet(n-1)
}
}
func main() {
fmt.Printf("5! = %d\n", fakultaet(5))
}
Das Gegenstück zur Rekursion ist die Iteration (lat. Wiederholung). Darunter versteht man die mehrfache Ausführung einer oder mehrerer Anweisungen (Schleifen).
Ein Algorithmus arbeitet in-place, wenn er außer dem für die Speicherung der zu bearbeitenden Daten benötigten Speicher nur eine konstante, also von der zu bearbeitenden Datenmenge unabhängige Menge von Speicher benötigt. Wenn die Ausgabedaten gesondert gespeichert und nicht die Eingabedaten damit überschrieben werden, arbeitet ein Algorithmus out-of-place. Der Speicherbedarf wächst dabei mit der zu bearbeitenden Datenmenge.
Unter der Komplexität (auch Aufwand oder Kosten) eines Algorithmus versteht man seinen maximalen Ressourcenbedarf. Wenn die betrachtete Ressource der Zeitaufwand für das Ausführen des Algorithmus ist, spricht man von der Laufzeitkomplexität.
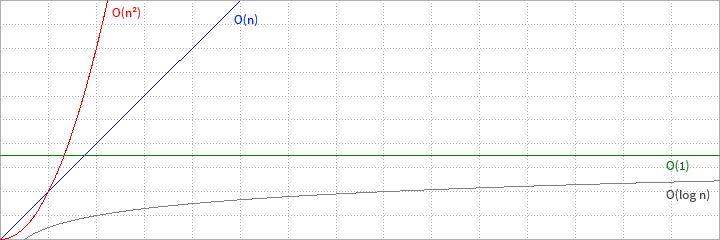
Der Zeitaufwand von Algorithmen lässt sich nicht eindeutig bestimmen. Zu viele Faktoren (Hardware, parallel laufende Prozesse, Eingabereihenfolge, ...) spielen eine Rolle, so dass mit herkömmlichen Mitteln keine genaue und allgemeine Aussage über die benötigte Zeit gemacht werden kann. Um dennoch Algorithmen vergleichen und in Klassen (konstant, logarithmisch, linear, exponentiell, u.a.) einteilen zu können werden nicht die benötigten Zeiten, sondern die "greifbaren" Elementarschritte bei einer bestimmten Eingabelänge n beschrieben. Die Ο-Notation (großes Omikron, auch Landau-Notation) beschreibt das Wachstumsverhalten eines Algorithmus (nicht eines Programms!) in Abhängigkeit von der Eingabegröße n.
Die Notation Ο(n) beschreibt beispielsweise ein einfaches lineares Wachstum. das bedeutet das die doppelte Anzahl Eingabewerte dazu führt das der Algorithmus doppelt so lange für die Verarbeitung benötigt. Ο(1) würde beschreiben das ein Algorithmus unabhängig von der Eingabegröße immer die gleiche Zeit benötigt und Ο(n²) würde ein quadratisches Wachstum beschreiben.

In der Regel werden die bestmögliche (Best-Case) und die schlechtestmögliche (Worst-Case) sowie die durchschnittliche (Average-Case) Konstellation an Eingabedaten betrachtet. Am Beispiel Lineare Suche soll verdeutlicht werden was damit gemeint ist. Angenommen die Eingabedatenmenge enthält die sechs Zahlen 5, 7, 6, 2, 1 und 3 in genau dieser Reihenfolge. Gesucht werden die Elemente 5, 3 und 2.
package main
import "fmt"
func search(haystack []int, needle int) int {
for i := 0; i < len(haystack); i++ {
if haystack[i] == needle {
return i
}
}
return -1
}
func main() {
var haystack = []int{5, 7, 6, 2, 1, 3}
fmt.Printf("5 at index %d\n", search(haystack, 5))
fmt.Printf("3 at index %d\n", search(haystack, 3))
fmt.Printf("2 at index %d\n", search(haystack, 2))
}
Im günstigsten Fall ist das gesuchte Element das erste Element in der Eingabedatenmenge, sodass nur ein einziger Schritt nötig ist um dessen Position zu ermitteln: Ο(1). Der ungünstigste Fall tritt auf wenn das gesuchte Element das letzte Element in der Eingabedatenmenge ist: Ο(n). Durchschnittlich dürfte das gesuchte Element nach Durchgang etwa der Hälfte aller Elemente gefunden werden: Ο(n/2).
Der Bubblesort (auch Sortieren durch Aufsteigen oder Austauschsortieren) ist ein iterativer Algorithmus, der vergleichsbasiert eine Liste von Elementen sortiert. Er arbeitet in-place, sortiert stabil und hat eine Laufzeit von Ο(n²) im schlimmsten (Worst-Case) wie auch im durchschnittlichen Fall (Average-Case).
bubblesort(array) {
n = count(array)
for n downto 1 {
i = 0
for i to n - 1 {
if array[i] > array[i+1] {
swap(array[i], array[i+1])
}
}
}
}
Der oben abgebildetet Variante des Bubblesort lästst sich noch weiter optimieren um eine Laufzeitkomplexität von Ο(n) im Best-Case zu erhalten.
bubblesort2(array) {
n = count(array)
i = 0
do {
swapped = false
for i to n - 1 {
if array[i] > array[i+1] {
swap(array[i], array[i+1])
swapped = true
}
}
n = n - 1
} while swapped == true
}
Die binäre Suche ist ein Algorithmus, der in einer Menge von Daten sehr effizient ein gesuchtes Element findet bzw. eine zuverlässige Aussage über das Fehlen dieses Elementes liefert. Voraussetzung ist das die Eingabedaten sortiert sind. Sortierung und spätere Suche müssen sich auf denselben Schlüssel beziehen. Der Algorithmus kann iterativ oder rekursiv implementiert werden und arbeitet in-place. Er hat im Average-Case und im Worst-Case ein Verhalten von Ο(log(n)).
package main
import "fmt"
func binarySearch(haystack []int, needle int) int {
var mitte, links, rechts = 0, 0, len(haystack) - 1
// Solange die zu durchsuchende Menge nicht leer ist
for links <= rechts {
// Bereich halbieren
mitte = links + ((rechts - links) / 2)
// Element needle gefunden?
if haystack[mitte] == needle {
return mitte
} else {
if haystack[mitte] > needle {
// im linken Abschnitt weitersuchen
rechts = mitte - 1
// haystack[mitte] < needle
} else {
// im rechten Abschnitt weitersuchen
links = mitte + 1
}
}
}
return -1
}
func main() {
var haystack = []int{1, 2, 3, 5, 6, 7}
fmt.Printf("5 at index %d\n", binarySearch(haystack, 5))
}
Daten zusammen mit der Definition aller zulässigen Operationen für den Zugriff werden in der Informatik auch als abstrakte Datentypen bezeichnet. Da der Zugriff nur über die festgelegten Operationen erfolgt, sind die Daten nach außen gekapselt. Ein abstrakter Datentyp beschreibt, was die Operationen tun (Semantik), aber noch nicht, wie sie es tun sollen (Implementierung). Stapelspeicher, Warteschlangen oder Listen können durch eine verkettete Liste implementiert werden.
| Datentyp | Beschreibung |
|---|---|
| List (Liste) | geordnete Sammlung von Elementen, welche jederzeit vergrößert oder verkleinert werden kann |
| Map (Assoziatives Array, Dictionary) | verwendet Schlüssel, um die enthaltenen Elemente zu adressieren; diese sind in keiner festgelegten Reihenfolge abgespeichert |
| Stack (Stapelspeicher) | push legt ein Element auf den Stapel und pop holt und entfernt das zuletzt auf den Stapel gelegte Element: LIFO (Last In - First Out) |
| Queue (Warteschlange) | Elemente werden in der Reihenfolge in der sie hinzugefügt wurden wieder aus der Warteschlange herausgeholt; Das zuerst eingereihte Element verlässt auch als ersten wieder die Warteschlange: FIFO (First In - First Out) |
Maps gibt es in der Programmiersprache Go als built-in Datentyp. Intern wird dieser Datentyp mit einer Hashtabelle realisiert. Bei der Verwendung einer Map müssen die Datentypen der Schlüssel (zwischen [ und ], nach dem Keyword map) sowie der Werte (hinter ]) angegeben werden.
var (
map1 map[string]string
map2 map[int]bool
)
Der Zugriff auf den Wert eines bestimmten Schlüssels erfolgt dann mit dem Index-Operator ([ ]). Eine Map muss vor der Verwendung mit der Funktion make() oder einem Map-Literal initialisiert worden sein, sonst Verursacht der Zugriff eine Panic.
var mymap = make(map[string]string)
var mymap2 = map[string]int{"a": 1, "b": 2, "c": 3}
mymap["key1"] = "value1"
Wenn auf den Wert eines Schlüssels zugegriffen wird der nicht in der Map vorhanden ist, dann wird der Nullwert des Wert-Datentyps zurückgegeben. Um unterscheiden zu können ob ein Schlüssel existiert oder nicht, wird beim Zugriff optional ein zweiter, Boolscher-Wert zurückgegeben. Existiert der Schlüssel gar nicht, ist dieser Wert false.
var (
value string
vorhanden bool
)
value, vorhanden = mymap["key2"]
Die Built-In-Funktion delete() löscht ein Schlüssel-Wert-Paar aus einer Map.
delete(mymap, "key to delete")
Mit der for-range-Schleife können außerdem alle Schlüssel-Wert-Paare nacheinander abgefragt werden.
for key, value := range mymap {
fmt.Print(key, value)
}
Eine einfach verkette Liste ist eine simple dynamische Datenstruktur. Zur Implementierung wird ein Listenelement (Node) mit zwei Feldern verwendet. Das erste Feld enthält die eigentlichen Daten bzw. einen Zeiger auf die Daten. Im zweiten Feld wird ein Zeiger auf das nächste Element der Kette gespeichert. Ein Listenelement das nicht auf ein weiteres Element der Kette zeigt markiert das Ende der verketteten Liste.

type node struct { data any; next *node }
type LinkedList struct { first *node }
Um ein bestimmtes Listenelement zu finden muss immer jedes Element vom ersten bis zum Letzten bzw. gefundenen Element durchlaufen werden. Zum Einfügen eines neuen Elementes müssen nur die Zeiger des vorhergehenden Elementes und des neuen Elementes angepasst werden. Es werden im Gegensatz zu einem Array beim Einfügen keine Elemente verschoben.
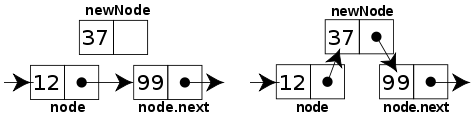
Zum Entfernen eines Elements aus der Kette wird der Zeiger auf das nächste Element des vorhergehenden Listenelements auf das dem zu löschenden Element nachfolgende Element gesetzt.

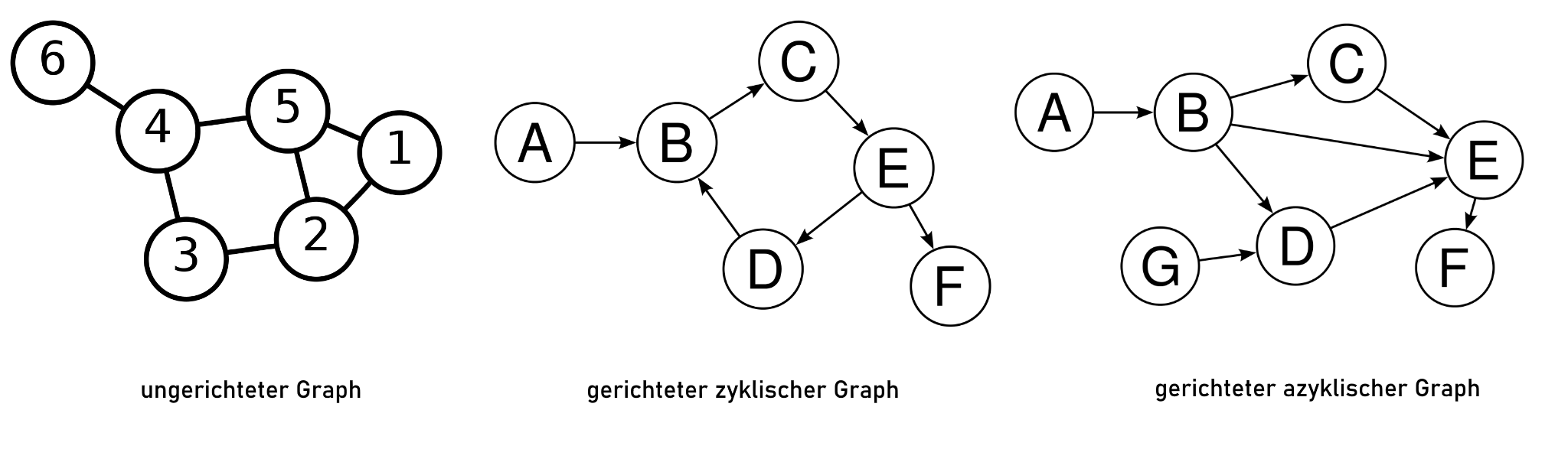
In der Informatik werden netzartige Strukturen die aus einer Menge von Knoten (engl. Node) und Kanten (engl. Edge) bestehen als Graphen bezeichnet. Die Graphentheorie als Teilgebiet der Mathematik und der theoretischen Informatik untersucht deren Eigenschaften und ihre Beziehungen zueinander. Es unterschiedliche Typen von Graphen. Wenn die Kanten zwischen den Knoten eine Richtung haben (dargetellt durch Pfeile) spricht man von einem gerichteten Graphnen ansonsten von einem ungerichteten Graphen. Wenn es bei gerichteten Graphen möglich ist, den Kantenrichtungen folgend, Knoten mehrmals bzw. immer wieder zu erreichen, dann spricht man von einem zyklischen Graphen. Bei Graphen wo das nicht möglich ist und es für alle Wege eine endliche Anzahl von Schritten gibt, nennt man azyklische Graphen.
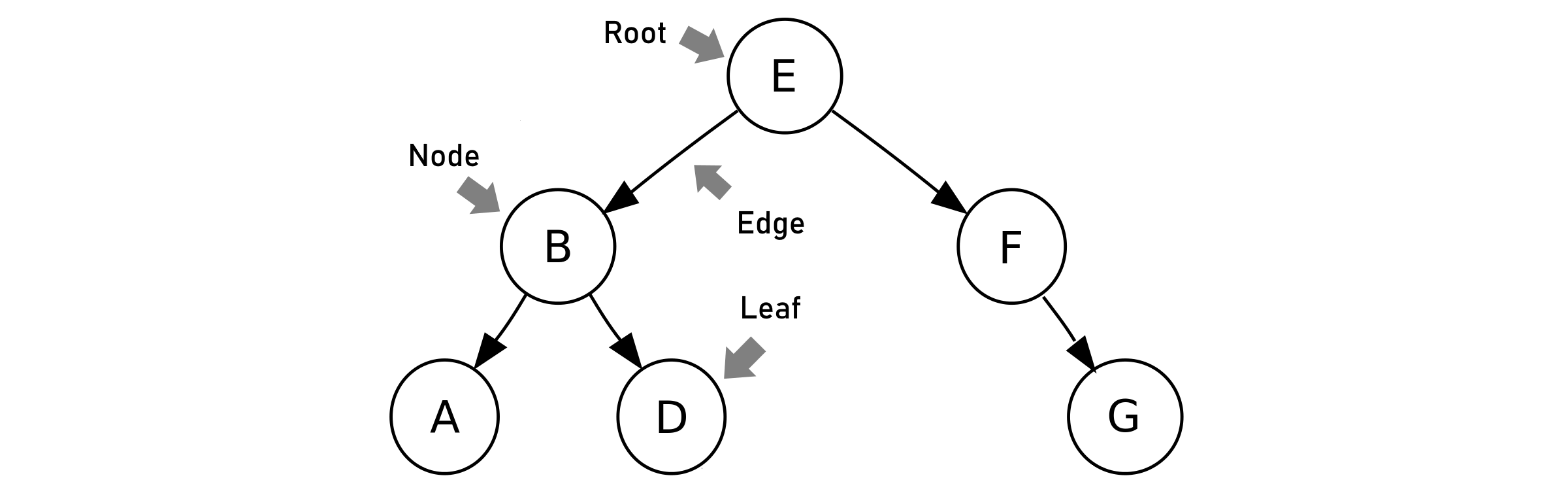
Ein spezieller Typ von Graphen sind Bäume (engl. Tree). Dabei handelt es sich um azyklische gerichtete Graphen die außerdem mit der Wurzel (engl. Root) einen Ausgangspunkt haben. Die Knoten welche keine weiteren Unterknoten besitzen werden auch Blätter (engl. Leaf) genannt. Der häufigste Untertyp ist wiederum ein Binärer Baum (engl. Binary Tree) bei dem jeder Knoten nur maximal zwei Unterknoten besitzen darf.